Zero Grads: Learning Local Surrogate Losses for Non-Differentiable Graphics

SIGGRAPH 2024

Michael Fischer, Tobias Ritschel
University College London


TLDR:

We learn a mapping between optimization parameters and their corresponding loss values, our neural surrogate loss, whose gradients we can then use for running gradient descent on arbitrary, high-dimensional black-box forward models.

Abstract:

Gradient-based optimization is now ubiquitous across graphics, but unfortunately can not be applied to problems with undefined or zero gradients. To circumvent this issue, the loss function can be manually replaced by a ``surrogate'' that has similar minima but is differentiable. Our proposed framework, ZeroGrads, automates this process by learning a neural approximation of the objective function, which in turn can be used to differentiate through arbitrary black-box graphics pipelines. We train the surrogate on an actively smoothed version of the objective and encourage locality, focusing the surrogate's capacity on what matters at the current training episode. The fitting is performed online, alongside the parameter optimization, and self-supervised, without pre-computed data or pre-trained models. As sampling the objective is expensive (it requires a full rendering or simulator run), we devise an efficient sampling scheme that allows for tractable run-times and competitive performance at little overhead. We demonstrate optimizing diverse non-convex, non-differentiable black-box problems in graphics, such as visibility in rendering, discrete parameter spaces in procedural modelling or optimal control in physics-driven animation. In contrast to other derivative-free algorithms, our approach scales well to higher dimensions, which we demonstrate on problems with up to 35k interlinked variables.

Method: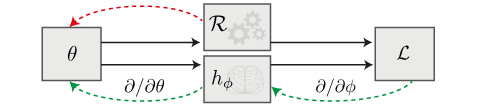

In ZeroGrads, we deal with the problem that many programs are not differentiable by design - for instance, as they're not written in a differentiable programming language, or simply were made for another user group (Photoshop, GIMP, ...). We therefore have no way of backpropagating through these programs (red arrow in the figure on the right). However, in this paper we show that we can still differentiate these programs if we can find a analytical mapping from the program input (the optimization parameters) to "how wrong" the output is, i.e., the loss function's value for these parameters. Once we have found such a mapping, we can use its gradients as "surrogate gradients" during gradient descent, and thus differentiate through non-differentiable programs (green arrows in the figure on the right) like Blender or Matplotlib.

However, it is often the case that large parts of this parameter space are irrelevant for the current optimization state, which is why we constrain our surrogate model to the local neighbourhood by sampling from a Gaussian. The surrogate therefore can "focus on what matters" at the current optimization step. In simple words, the four key steps in ZeroGrads are:
  1. Smooth the loss landscape via convolution with a Gaussian kernel, a trick introduced in PRDPT.
  2. Locally sample around the current parameter state to produce samples for our surrogate fitting.
  3. Fit an analytical function (we use an MLP) to these samples.
  4. Compute the gradient of the MLP w.r.t. the optimization parameters, and use this gradient to perform an (Adam-) gradient descent step.
We provide a Colab Notebook that shows a simple example and how ZeroGrads outperforms its competitors.

Results:
We compare our method against the traditional derivative-free optimizers Simulated Annealing (SA), Genetic Algorithms (GA), Simultaneous Perturbation Stochastic Spproximation (SPSA), Covariance Matrix Adaption Evolutionary Strategy (CMA-ES), and our previously published gradient estimator PRDPT, here denoted as FR22.

In this experiment, we optimize a heightfield such that the resulting caustic matches a reference. The heightfield is parametrized as a 1,024-dimensional spline.


Here, we optimize the 196,608 color values of a 256x256 RGB texture. CMA-ES cannot be run on this example due to its quadratic memory complexity.


In this example, we optimize the 35,152 weights of an MLP such that it encodes digits from the MNIST dataset.


In this inverse rendering scenario, the task is to deform a tesselated sphere into a mesh that explains the reference views. "Diff. Rendering" implements the Largesteps approach by Nicolet et al., 2021.


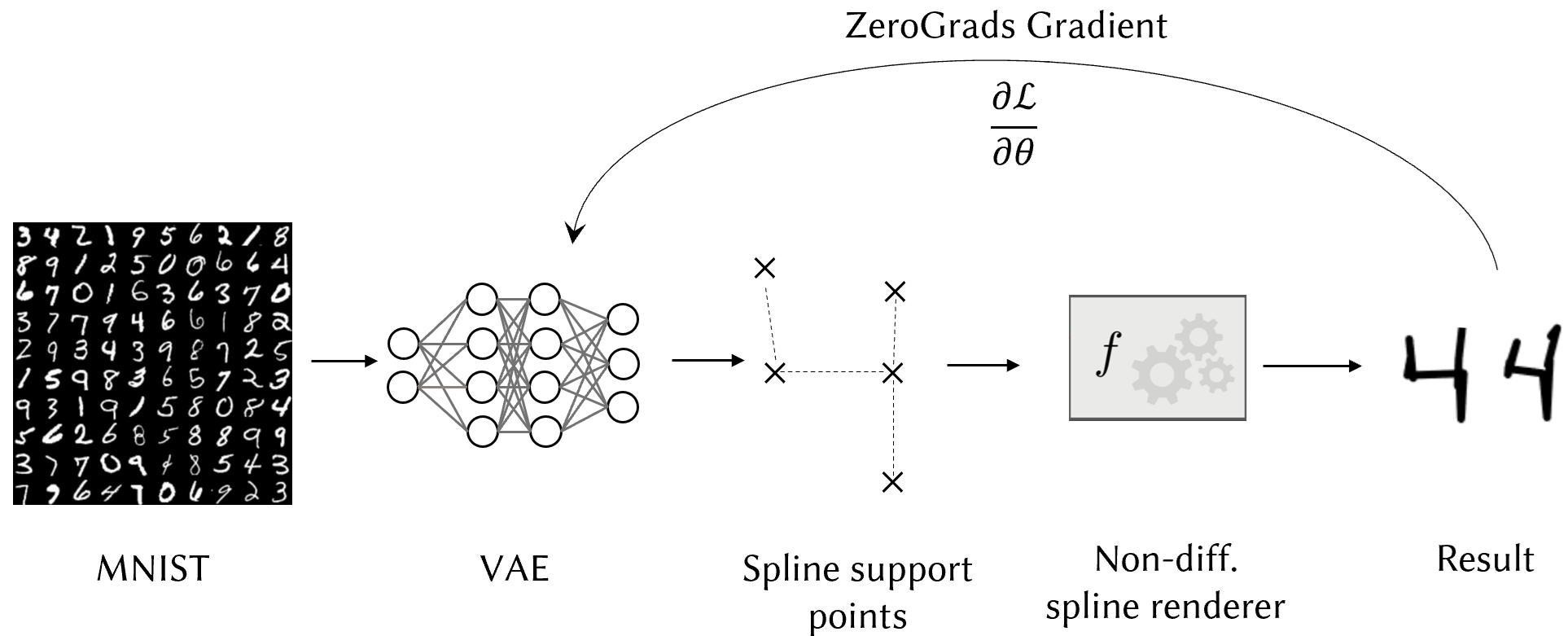
Finally, in this example, we train a generative model on a non-differentiable task. Specifically, we use a VAE that learns to encode digits from the MNIST dataset. However, instead of simply decoding the latents to pixel values, the VAE produces spline-support-points, which are then rendered with a non-differentiable spline renderer (see the figure on the right for a schematic). We use a weighted mixture of MSE and KLD as the trainig loss and backpropagate this loss through the non-diff. spline renderer (i.e., from the rendered spline to the VAE weights) using our proposed method ZeroGrads. The below digits are samples from the latent space of the trained VAE, in a variety of styles, which are easily applicable in post-processing thanks to the spline formulation.


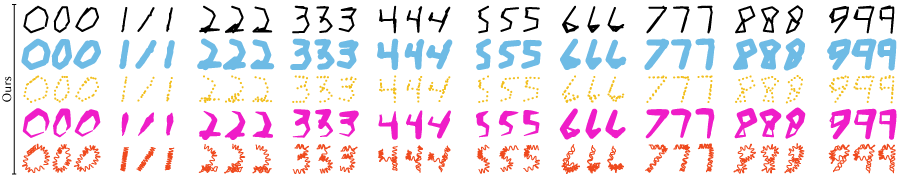
The magic that makes our approach scale to high dimensions is the surrogate's hysteresis, which reduces the gradient variance. In contrast to methods that re-build a linear gradient estimate from scratch at every optimization iteration, the MLP's spectral bias prevents rapid changes and thus achieves a smoother gradient trajectory over time. We plan to explore this further in future research.

Citation
If you find our work useful and use parts or ideas of our paper or code, please cite:

@article{fischer2024zerograds,
  title={ZeroGrads: Learning Local Surrogates for Non-Differentiable Graphics},
  author={Fischer, Michael and Ritschel, Tobias},
  journal={ACM Transactions on Graphics (TOG)},
  volume={43},
  number={4},
  pages={1--15},
  year={2024},
  publisher={ACM New York, NY, USA}
}

Acknowledgements
We extend our gratitude to the anonymous reviewers for their insightful feedback and to Meta Reality Labs for their continuous support. Additionally, we are thankful for the support provided by the Rabin Ezra Scholarship Trust.